Haber-Utku ÇELİK
Çocukların çarpım tablosunu öğrenirken sıkılmaması için çeşitli yöntemler kullanılabilir. Örneğin, çarpım tablosunu şarkı haline getirerek ezberlemek, oyunlar oynayarak öğrenmek veya renkli ve ilgi çekici grafikler kullanarak görsel hafızayı güçlendirmek gibi yöntemler uygulanabilir.
Ayrıca, çarpım tablosu öğrenme sürecinde çocukların anlaması için gerçek hayat örnekleri de kullanılabilir. Örneğin, 3 çocuğun her birinin 4 elması olduğunda kaç tane elma olduğunu hesaplamak gibi basit örneklerle çocuklar matematik kavramlarını daha iyi anlayabilirler.
Sonuç olarak, çarpım tablosu öğrenme süreci sıkıcı bir aktivite olmaktan çıkarılabilir ve çocukların matematikle ilgili tutkularını geliştirmeleri için eğlenceli bir fırsata dönüştürülebilir. Bu sayede, çocuklar matematiksel düşünme becerilerini geliştirerek gelecekte daha başarılı bir hayat sürdürebilirler.

ÇARPIM TABLOSU

1'LER ÇARPIM TABLOSU
1 x 1 = 1
1 x 2 = 2
1 x 3 = 3
1 x 4 = 4
1 x 5 = 5
1 x 6 = 6
1 x 7 = 7
1 x 8 = 8
1 x 9 = 9
1 x 10 = 10

2'LER ÇARPIM TABLOSU
2 x 1 = 2
2 x 2 = 4
2 x 3 = 6
2 x 4 = 8
2 x 5 = 10
2 x 6 = 12
2 x 7 = 14
2 x 8 = 16
2 x 9 = 18
2 x 10 = 20

3'LER ÇARPIM TABLOSU
3 x 1 = 3
3 x 2 = 6
3 x 3 = 9
3 x 4 = 12
3 x 5 = 15
3 x 6 = 18
3 x 7 = 21
3 x 8 = 24
3 x 9 = 27
3 x 10 = 30

4'LER ÇARPIM TABLOSU
4 x 1 = 4
4 x 2 = 8
4 x 3 = 12
4 x 4 = 16
4 x 5 = 20
4 x 6 = 24
4 x 7 = 28
4 x 8 = 32
4 x 9 = 36
4 x 10 = 40

5'LER ÇARPIM TABLOSU
5 x 1 = 5
5 x 2 = 10
5 x 3 = 15
5 x 4 = 20
5 x 5 = 25
5 x 6 = 30
5 x 7 = 35
5 x 8 = 40
5 x 9 = 45
5 x 10 = 50

6'LAR ÇARPIM TABLOSU
6 x 1 = 6
6 x 2 = 12
6 x 3 = 18
6 x 4 = 24
6 x 5 = 30
6 x 6 = 36
6 x 7 = 42
6 x 8 = 48
6 x 9 = 54
6 x 10 = 60

7'LER ÇARPIM TABLOSU
7 x 1 = 7
7 x 2 = 14
7 x 3 = 21
7 x 4 = 28
7 x 5 = 35
7 x 6 = 42
7 x 7 = 49
7 x 8 = 56
7 x 9 = 63
7 x 10 = 70

8'LER ÇARPIM TABLOSU
8 x 1 = 8
8 x 2 = 16
8 x 3 = 24
8 x 4 = 32
8 x 5 = 40
8 x 6 = 48
8 x 7 = 56
8 x 8 = 64
8 x 9 = 72
8 x 10 = 80

9'LAR ÇARPIM TABLOSU
9 x 1 = 9
9 x 2 = 18
9 x 3 = 27
9 x 4 = 36
9 x 5 = 45
9 x 6 = 54
9 x 7 = 63
9 x 8 = 72
9 x 9 = 81
9 x 10 = 90
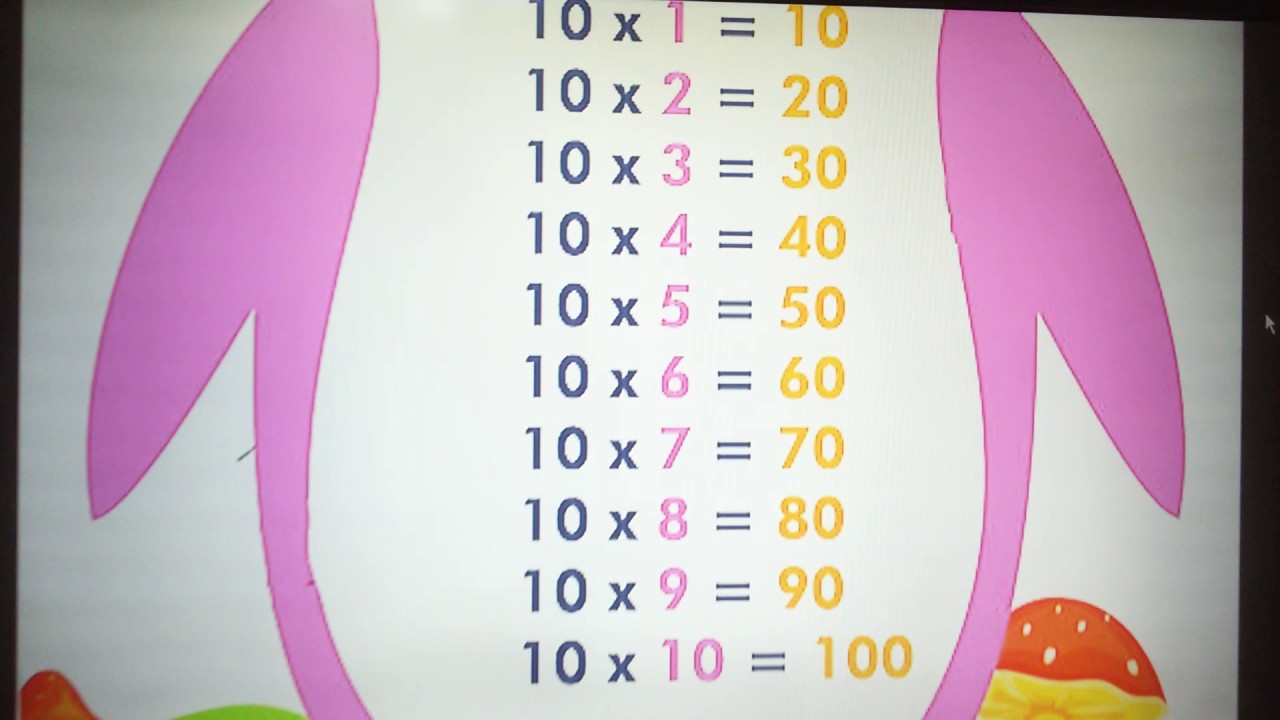
10'LAR ÇARPIM TABLOSU
10 x 1 = 10
10 x 2 = 20
10 x 3 = 30
10 x 4 = 40
10 x 5 = 50
10 x 6 = 60
10 x 7 = 70
10 x 8 = 80
10 x 9 = 90
10 x 10 = 100
ÇARPIM TABLOSU EZBERLEME HANGİ YÖNTEMLERLE YAPILIR?
Çarpım tablosu öğrenmek için kullanılan ezberleme teknikleri, çocuklara eğlendirici ve akılda kalıcı bilgiler sunarak sayılarla uyumlu hale getirmeyi amaçlamaktadır. Örneğin, "4 defa 8 eşittir 32, çok kurnazdır tilki" veya "2 kere 6 eşittir 12, tabakta yemek bırakılmaz ki" gibi tekerlemeler, çocukların zihninde aktif bir öğrenme süreci başlatarak matematik kavramlarını kalıcı hale getirmelerine yardımcı olabilir.
Ayrıca, çocukların ilgi alanlarına uygun müzikli çarpım tablosu videolarını bulabilecekleri sosyal medya ve mobil uygulamaları da kullanabilirsiniz. Bu sayede, çocuklar eğlenceli ve yaratıcı bir şekilde matematik öğrenerek sayılarla uyum sağlayabilirler.
Özetle, çarpım tablosu öğrenmek için kullanılan ezberleme teknikleri çocukların öğrenme sürecini eğlenceli ve ilgi çekici hale getirerek sayıların kalıcı hafızaya kazınmasını sağlar. Bu sayede çocuklar matematik kavramlarını daha iyi anlayarak, ileriki yaşamlarında da başarılı bir şekilde kullanabilirler.
ÇARPIM TABLOSU EZBERLEMENİN PÜF NOKTALARI NELERDİR?
Çarpım tablosu ezberlemenin püf noktaları şu şekilde sıralanmıştır:
- Çarpma işleminde, çarpılan sayıların sıralaması önemli değildir. Örneğin 7x5=35 ile 5x7=35 aynı sonucu verir ve bu özellik birçok sayının hızlı ve kolay bir şekilde öğrenilmesine yardımcı olabilir.
- Sıfır ile herhangi bir sayı çarpıldığında sonuç her zaman sıfırdır. Bu özelliği çocuğunuza "sıfırın boş bir mide" olduğu şeklinde anlatarak diğer sayıları yutarak hiçbir şey bırakmadığını vurgulayabilirsiniz. Örneğin, 8x0=0 kuralı gibi benzer hikayelerle çarpım tablosu ezberleme işlemi yapılabilir.
- Herhangi bir sayı ile çarpıldığında, sonuç çarpılan sayıya eşittir. Örneğin 9x1=9.
- İki sayı her zaman sayının iki katını verir. Bu özellik sayının kendisi ile toplandığında sonucun iki katına tekabül eder. Örneğin: 3x2=6, 4x2=8, 2x2=4.
- 5 sayısı ile çarpılan herhangi bir sayının birler basamağı ya 0 ya da 5'tir. Örneğin 5x5=25, 5x8=40, 9x5=45 gibi.
- Dokuz rakamı ile çarpılan sayıların birler basamağı sırasıyla 9,8,7,6,5 vb. şeklinde devam eder. Örneğin: 9,18,27,36,45,54,63,72,81,90.
- 10 sayısı ile çarpılan herhangi bir sayının birler basamağı her zaman sıfırdır. Örneğin 10x2=20, 4x10=40, 40x2=80 gibi.
PİSAGOR TABLOSU YÖNTEMİ ÇARPIM TABLOSUNUN ÖĞRENMEDE NEDEN DAHA ETKİLİDİR?
Çocuklara matematik öğretirken Pisagor tablosu yöntemini kullanmak, ezbercilik yerine düşünme becerilerini teşvik ederek öğrenmeyi kalıcı hale getirebilir. Pisagor tablosu, çocuğun sayıları kolayca öğrenip kavramasına yardımcı olur. Özellikle hafızası güçlü olan çocuklar, uzun matematik formüllerini bile kolay ve hızlı bir şekilde öğrenebilirler.
Pisagor tablosu kullanarak daha az bilgiyle sayıları rahatlıkla ezberlemek mümkündür. İnsan beyni, simetriyi otomatik olarak algılayıp kalıcı bir şekilde öğrenmeye adapte edilmiştir. Bu nedenle, Pisagor tablosu ile öğretilen çarpım tablosu, çocuğunuzun rahat ve hızlı bir şekilde öğrenmesine yardımcı olabilir.
ÇARPIM TABOSU HIZLICA NASIL ÖĞRENİLİR?
Çocukların çarpım tablosunu hızlı bir şekilde öğrenmeleri için öncelikle 1’ den 10 ’a kadar olan tabloyu, rakamları 1’ den başlayarak ezberlemeleri önemlidir. Ancak sadece ezberlemek değil, her bir rakamın kendisiyle çarpıldığında sonucun kendisine eşit olduğu kavratılmalıdır. Daha sonra, 2’ler, 3’ler, 4’ler gibi ayrı ayrı çarpım tabloları yazılarak öğrenme süreci kolaylaştırılabilir.
Ezberleme sürecinde çarpım tabloları sesli bir şekilde tekrar edilmeli ve bu sayede öğrenme süreci daha kalıcı hale getirilmelidir. En son aşamada, tüm çarpım tablosu toplu olarak yazılıp, karmaşık alıştırmalar yapılarak öğrenme süreci pekiştirilmelidir. Ezber işlemi tekrarlandıkça, kavrama da artarak, beyin daha kolay ve hızlı bir şekilde öğrenmeye adapte olacaktır.
Ezberciliği dayatmadan, çarpım tablosunu kavramaları için çocukların düşünmeleri teşvik edilmelidir. Bunun için, çarpım tablosu yöntemini kullanan Pisagor tablosu gibi yöntemler de kullanılabilir. Pisagor tablosu, simetriyi kullanarak çarpım tablosunu daha kolay bir şekilde öğrenmelerine yardımcı olur. Simetriyi algılaması daha kolay olan insan beyni, çarpım tablosunu da daha kolay ve hızlı bir şekilde öğrenmeye adaptasyon sağlayacaktır.










